练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若直线l的方程为x=2，则该直线的倾斜角是（　　）
    A．60°B．45°C．90°D．180°
    C
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    1、若直线l的方程为x=2，则该直线的倾斜角是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    若直线l的方程为x=2，则该直线的倾斜角是（　　）
    A．60°B．45°C．90°D．180°

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年福建省三明市五校联考高二（上）期中数学试卷（必修2）（解析版） 题型：选择题

    若直线l的方程为x=2，则该直线的倾斜角是（ ）
    A．60°
    B．45°
    C．90°
    D．180°

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若直线l的方程为x=2，则该直线的倾斜角是


    1. A.
      60°
    2. B.
      45°
    3. C.
      90°
    4. D.
      180°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若直线l经过两条直线2x-3y-3=0和x+y+2=0的交点，且与直线3x+y-1=0平行，则该直线l方程为
    15x+5y+16=0
    15x+5y+16=0
    ．

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年江苏省南京师大附中高三（上）第二次段考数学试卷（解析版） 题型：填空题

    若直线l经过两条直线2x-3y-3=0和x+y+2=0的交点，且与直线3x+y-1=0平行，则该直线l方程为    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    若直线l经过两条直线2x-3y-3=0和x+y+2=0的交点，且与直线3x+y-1=0平行，则该直线l方程为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    22.已知复数z0＝l－mi（m>0），z=x+yi和w=x′+y′i.其中x，y，x′,y′均为实数.i为虚数单位，且对于任意复数z，有w=·，.

    （1）试求m的值，并分别写出x′和y′用x、y表示的关系式；

    （2）将（x，y）作为点P的坐标，（x′，y′）作为点Q的坐标，上述关系式可以看作是坐标平面上点的一个变换：它将平面上的点P变到这一平面上的点Q.

    当点P在直线y=x+1上移动时，试求点P经该变换后得到的点Q的轨迹方程.

    （3）是否存在这样的直线：它上面的任一点经上述变换后得到的点仍在c 该直线上？若存在，试求出所有这些直线；若不存在，则说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    选做题（请考生从以下三个小题中任选一个作答，若多选，则按所选的第一题计分．）
    A（坐标系与参数方程选讲选做题）直线l：
    x=4t
    y=3t-2
    （t为参数）被曲线C：
    x=5+2cosθ
    y=3+2sinθ
    （θ为参数）所截得的弦长为
    2
    		3
    2
    		3
    ．
    B（不等式选讲选做题）若存在实数x满足|x-3|+|x-m|＜5，则实数m的取值范围为
    -2＜m＜8
    -2＜m＜8
    ．
    C（几何证明选讲选做题）若一直角三角形的内切圆与外接圆的面积分别π与9π，则该三角形的面积为
    7
    7
    ．

    查看答案和解析>>

    科目：高中数学 来源：2011年上海市徐汇区高考数学三模试卷（文科）（解析版） 题型：解答题

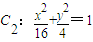    定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆．
    （1）若椭圆，判断C2与C1是否相似？如果相似，求出C2与C1的相似比；如果不相似，请说明理由；
    （2）写出与椭圆C1相似且短半轴长为b的椭圆Cb的方程；若在椭圆Cb上存在两点M、N关于直线y=x+1对称，求实数b的取值范围？
    （3）如图：直线l与两个“相似椭圆”和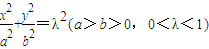分别交于点A，B和点C，D，证明：|AC|=|BD|

    查看答案和解析>>


    同步练习册答案