
科目:高中数学 来源: 题型:
| f(x)•f(y)+1 | f(y)-f(x) |
科目:高中数学 来源: 题型:
| f(x)•f(y)+1 |
| f(y)-f(x) |
科目:高中数学 来源: 题型:
已知函数f(x)的定义域为{x| x ≠ kπ,k ∈ Z},且对于定义域内的任何x、y,有f(x?? - y) = ![]() 成立,且f(a) = 1(a为正常数),当0 < x < 2a时,f(x) > 0.(I)判断f(x)奇偶性;(II)证明f(x)为周期函数;(III)求f (x)在[2a,3a] 上的最小值和最大值.
成立,且f(a) = 1(a为正常数),当0 < x < 2a时,f(x) > 0.(I)判断f(x)奇偶性;(II)证明f(x)为周期函数;(III)求f (x)在[2a,3a] 上的最小值和最大值.
科目:高中数学 来源:汕头市2009-2010学年度第二学期高三级数学综合测练题(理三) 题型:解答题
已知函数f(x)的定义域为{x| x ≠ kπ,k ∈ Z},且对于定义域内的任何x、y,有f(x - y) = 成立,且f(a) = 1(a为正常数),当0 < x < 2a时,f(x) > 0.
(1)判断f(x)奇偶性;
(2)证明f(x)为周期函数;
(3)求f (x)在[2a,3a] 上的最小值和最大值.
科目:高中数学 来源:不详 题型:解答题
| f(x)•f(y)+1 |
| f(y)-f(x) |
科目:高中数学 来源:同步题 题型:解答题
科目:高中数学 来源:2006-2007学年北京市清华附中高三(上)10月月考数学试卷(理科)(解析版) 题型:解答题
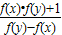 成立,且f(a)=1(a为正常数),当0<x<2a时,f(x)>0.
成立,且f(a)=1(a为正常数),当0<x<2a时,f(x)>0.科目:高中数学 来源:2012-2013学年黑龙江省大庆市铁人中学高一(上)期末数学试卷(解析版) 题型:解答题
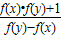 成立,且f(a)=1(a为正常数),当0<x<2a时,f(x)>0.
成立,且f(a)=1(a为正常数),当0<x<2a时,f(x)>0.科目:高中数学 来源:2010-2011学年四川省成都九中高三(下)3月月考数学试卷(理科)(解析版) 题型:选择题
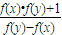 成立,且f(a)=1(a为正常数),当0<x<2a时,f(x)>0则( )
成立,且f(a)=1(a为正常数),当0<x<2a时,f(x)>0则( )科目:高中数学 来源:2009年高考数学压轴试卷集锦(3)(解析版) 题型:解答题
 成立,且f(a)=1(a为正常数),当0<x<2a时,f(x)>0.
成立,且f(a)=1(a为正常数),当0<x<2a时,f(x)>0.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com