
科目:高中数学 来源:不详 题型:单选题
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
A.
| B.
| C.
| D.
|
科目:高中数学 来源:不详 题型:单选题
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
A.
| B.
| C.
| D.
|
科目:高中数学 来源:2012-2013学年福建省泉州市德化一中高二(下)第二次质检数学试卷(理科)(解析版) 题型:选择题
 ,则P(B|A)=( )
,则P(B|A)=( )



科目:高中数学 来源:2011-2012学年福建省福州八中高二(下)期末数学试卷(理科)(解析版) 题型:选择题
 ,则P(B|A)=( )
,则P(B|A)=( )



科目:高中数学 来源: 题型:
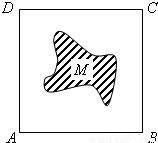
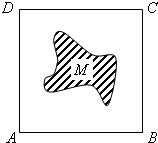 如图,面积为S的正方形ABCD中有一个不规则的图形M,可按下面方法估计M的面积:在正方形ABCD中随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为
如图,面积为S的正方形ABCD中有一个不规则的图形M,可按下面方法估计M的面积:在正方形ABCD中随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为| m |
| n |
| k |
 |
| t=0 |
| C | t 10000 |

科目:高中数学 来源:海南省高考真题 题型:解答题
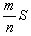 。假设正方形ABCD的边长为2,M的面积为1,并向正方形ABCD中随机投掷10000个点,以X表示落入M中的点的数目,
。假设正方形ABCD的边长为2,M的面积为1,并向正方形ABCD中随机投掷10000个点,以X表示落入M中的点的数目,
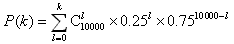
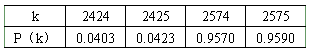
科目:高中数学 来源:2010-2011学年山西省太原五中高三(下)3月月考数学试卷(理科)(解析版) 题型:解答题
 .假设正方形ABCD的边长为2,M的面积为1,并向正方形ABCD中随机投掷10000个点,以X表示落入M中的点的数目.
.假设正方形ABCD的边长为2,M的面积为1,并向正方形ABCD中随机投掷10000个点,以X表示落入M中的点的数目.

科目:高中数学 来源:2010年广东省江门市高考数学后阶段备考指导和猜题试卷(解析版) 题型:解答题
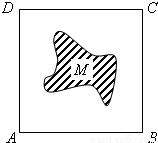
 .假设正方形ABCD的边长为2,M的面积为1,并向正方形ABCD中随机投掷10000个点,以X表示落入M中的点的数目.
.假设正方形ABCD的边长为2,M的面积为1,并向正方形ABCD中随机投掷10000个点,以X表示落入M中的点的数目.


科目:高中数学 来源:2011年高考数学综合复习试卷(2)(解析版) 题型:解答题
 .假设正方形ABCD的边长为2,M的面积为1,并向正方形ABCD中随机投掷10000个点,以X表示落入M中的点的数目.
.假设正方形ABCD的边长为2,M的面积为1,并向正方形ABCD中随机投掷10000个点,以X表示落入M中的点的数目.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com