
科目:高中数学 来源:不详 题型:单选题
| A.f(x)=3x | B.f(x)=x3 | C.f(x)=3x | D.y=log3x |
科目:高中数学 来源:2012-2013学年福建省厦门大学附属科技中学高一(上)期中数学试卷(解析版) 题型:选择题
科目:高中数学 来源: 题型:单选题
科目:高中数学 来源:0113 期中题 题型:单选题
科目:高中数学 来源:北京师大附中2011-2012学年高一上学期期末考试数学试题 题型:044
函数f(x)的定义域关于原点对称,但不包括数0,对定义域中的任意实数x,在定义域中存在x1,x2使x=x1-x2,,f(x1)≠f(x2),且满足以下3个条件.
(1)x1,x2是f(x)定义域中的数,f(x1)≠f(x2),则f(x1-x2)=![]()
(2)f(a)=1,(a是一个正的常数)
(3)当0<x<2a时,f(x)>0.
证明:(1)f(x)是奇函数;
(2)f(x)是周期函数,并求出其周期;
(3)f(x)在(0,4a)内为减函数.
科目:高中数学 来源: 题型:
| f(x1)+f(x2) |
| 2 |
科目:高中数学 来源:2012-2013学吉林省吉林市高三(上)开学摸底数学试卷 (理科)(解析版) 题型:选择题
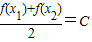 成立(其中C为常数),则称函数y=f(x)在D上的约算术均值为C,则下列函数在其定义域上的算术均值可以为2的函数是( )
成立(其中C为常数),则称函数y=f(x)在D上的约算术均值为C,则下列函数在其定义域上的算术均值可以为2的函数是( )科目:高中数学 来源: 题型:单选题
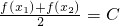 成立(其中C为常数),则称函数y=f(x)在D上的约算术均值为C,则下列函数在其定义域上的算术均值可以为2的函数是
成立(其中C为常数),则称函数y=f(x)在D上的约算术均值为C,则下列函数在其定义域上的算术均值可以为2的函数是科目:高中数学 来源: 题型:填空题
已知函数f(x)的定义域为R,且f(x)不为常值函数,有以下命题:
①函数g(x)=f(x)+f(-x)一定是偶函数;
②若对任意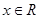 都有
都有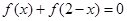 ,则f(x)是以2为周期的周期函数;
,则f(x)是以2为周期的周期函数;
③若f(x)是奇函数,且对任意x∈R都有f(x)+f(2+x)=0,则f(x)的图像的对称轴方程为
x=2n+1(n∈Z);
④对任意x1,x2∈R且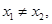 若
若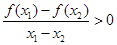 恒成立,则f(x)为
恒成立,则f(x)为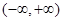 上的增函数.
上的增函数.
其中所有正确命题的序号是________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com