练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数y=f（x）满足f（2）＞f（1），f（1）＜f（0）则下列选项中正确的是（　　）
    A．函数y=f（x）在[1，2]是减函数，在[0，1]上是增函数
    B．函数y=f（x）在[1，2]是增函数，在[0，1]上是减函数
    C．函数y=f（x）在[0，2]上的最小值是f（1）
    D．以上都不正确
    D
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：单选题

    已知函数y=f（x）满足f（2）＞f（1），f（1）＜f（0）则下列选项中正确的是


    1. A.
      函数y=f（x）在[1，2]是减函数，在[0，1]上是增函数
    2. B.
      函数y=f（x）在[1，2]是增函数，在[0，1]上是减函数
    3. C.
      函数y=f（x）在[0，2]上的最小值是f（1）
    4. D.
      以上都不正确

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    12、已知函数y=f（x）（定义域为D，值域为A）有反函数y=f--1（x），则方程f（x）=0有解x=a，且f（x）＞x（x∈D）的充要条件是y=f--1（x）满足
    f--1（0）=a，且f--1（x）＜x（x∈A）/y=f--1（x）的图象在直线y=x的下方，且与y轴的交点为（0，a）…
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数y=f（x）在R上可导，满足xf′（x）＞-f（x），若a＞b，则下列不等式一定成立的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省台州市天台县育青中学高二（下）第一次月考数学试卷（理科）（解析版） 题型：选择题

    已知函数y=f（x）在R上可导，满足xf′（x）＞-f（x），若a＞b，则下列不等式一定成立的是（ ）
    A．af（b）＞bf（a）
    B．af（a）＞bf（b）
    C．af（b）＜bf（a）
    D．af（a）＞bf（b）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=（
    1
    2
    ）x-log3x，正实数a，b，c是公差为正实数的等差数列，且满足f（a）•f（b）•f（c）＞0；已知命题P：实数d是函数y=f（x）的一个零点；则下列四个命题：①d＜a；②d＞b；③d＜c；④d＞c中是命题P的必要不充分条件的命题个数为（　　）

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖南省、岳阳县一中高三11月联考理科数学 题型：选择题

    已知函数f(x)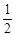＝()x－log3x，正实数a,b,c是公差为正实数的等差数列，且满足f(a)·f(b)·f(c)>0；已知命题P：实数d是函数y=f(x)的一个零点；则下列四个命题：①d＜a；②d＞b；③d＜c；④d＞c中是命题P的必要不充分条件的命题个数为（      ）

    A．1               B．2               C． 3             D．4

     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知函数f(x)＝()x－log3x，正实数a,b,c是公差为正实数的等差数列，且满足f(a)·f(b)·f(c)>0；已知命题P：实数d是函数y=f(x)的一个零点；则下列四个命题：①d＜a；②d＞b；③d＜c；④d＞c中是命题P的必要不充分条件的命题个数为（     ）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源：2012届湖南省澧县一中、岳阳县一中高三11月联考理科数学 题型：单选题

    已知函数f(x)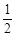＝()x－log3x，正实数a,b,c是公差为正实数的等差数列，且满足f(a)·f(b)·f(c)>0；已知命题P：实数d是函数y=f(x)的一个零点；则下列四个命题：①d＜a；②d＞b；③d＜c；④d＞c中是命题P的必要不充分条件的命题个数为（     ）

    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省重点中学高一（上）期中数学试卷（解析版） 题型：解答题

    若函数f（x）对定义域中任意x，均满足f（x）+f（2a-x）=2b，则称函数y=f（x）的图象关于点（a，b）对称；
    （1）已知的图象关于点（0，1）对称，求实数m的值；
    （2）已知函数g（x）在（-∞，0）∪（0，+∞）上的图象关于点（0，1）对称，且当x∈（0，+∞）时，g（x）=-2x-n（x-1），求函数g（x）在x∈（-∞，0）上的解析式；
    （3）在（1）（2）的条件下，若对实数x＜0及t＞0，恒有g（x）+tf（t）＞0，求正实数n的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年北京市十一学校高三（上）暑期检测数学试卷1（文科）（解析版） 题型：解答题

    若函数f（x）对定义域中任意x均满足f（x）+f（2a-x）=2b，则称函数y=f（x）的图象关于点（a，b）对称．
    （Ⅰ）已知函数的图象关于点（0，1）对称，求实数m的值；
    （Ⅱ）已知函数g（x）在（-∞，0）∪（0，+∞）上的图象关于点（0，1）对称，且当x∈（0，+∞）时，g（x）=x2+ax+1，求函数g（x）在（-∞，0）上的解析式；
    （Ⅲ）在（Ⅰ）、（Ⅱ）的条件下，当t＞0时，若对任意实数x∈（-∞，0），恒有g（x）＜f（t）成立，求实数a的取值范围．

    查看答案和解析>>


    同步练习册答案