
科目:高中数学 来源:不详 题型:单选题
| π |
| 2 |
| A.y=sin|x| | B.y=cos|x| | C.y=|
| D.y=lg|sinx| |
科目:高中数学 来源:不详 题型:单选题
| π |
| 2 |
| A.y=sin|x| | B.y=cos|x| | C.y=|
| D.y=lg|sinx| |
科目:高中数学 来源:2012-2013学年正大学校高三(上)周练数学试卷(10)(理科)(解析版) 题型:选择题
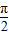 )上单调递增的偶函数是( )
)上单调递增的偶函数是( )
科目:高中数学 来源: 题型:
| π |
| 2 |
| A、y=cos2x | ||
| B、y=2|sinx| | ||
C、y=(
| ||
| D、y=-cotx |
科目:高中数学 来源: 题型:
| 3π |
| 2 |
| A、y=-tanx |
| B、y=cos2x |
| C、y=2sinx |
| D、y=|sinx| |
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 2 |
| A、①②③ | B、②③④ |
| C、①③④ | D、①②③④ |
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
| π |
| 12 |
| π |
| 3 |
| π |
| 6 |
| A、①②⇒③④ |
| B、③④⇒①② |
| C、②④⇒①③ |
| D、①③⇒②④ |
科目:高中数学 来源:河北省高三下学期第二次考试数学(理) 题型:选择题
设函数 是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足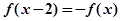 对一切
对一切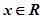 恒成立,当
恒成立,当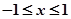 时,
时,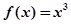 .则下列四个命题中正确的命题是( )
.则下列四个命题中正确的命题是( )
①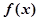 是以4为周期的周期函数;②
是以4为周期的周期函数;②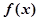 在
在 上的解析式为
上的解析式为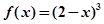 ;
;
③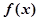 图象的对称轴中有
图象的对称轴中有 ;④
;④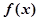 在
在 处的切线方程为
处的切线方程为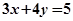 .
.
A、①②③ B、②③④ C、①③④ D、①②③④
科目:高中数学 来源:河北省正定中学2010高三下学期第二次考试(理) 题型:选择题
设函数 是定义域为R的奇函数,且满足
是定义域为R的奇函数,且满足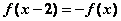 对一切
对一切 恒成立,当
恒成立,当 时,
时,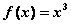 .则下列四个命题中正确的命题是( )
.则下列四个命题中正确的命题是( )
①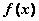 是以4为周期的周期函数;②
是以4为周期的周期函数;②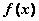 在
在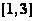 上的解析式为
上的解析式为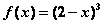 ;
;
③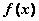 图象的对称轴中有
图象的对称轴中有 ;④
;④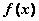 在
在 处的切线方程为
处的切线方程为 .
.
A、①②③ B、②③④ C、①③④ D、①②③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com