
科目:高中数学 来源: 题型:
 如图所示,在△ABC中,BC边上的两点D、E分别与A连线,假设∠ACB=∠ADC=
如图所示,在△ABC中,BC边上的两点D、E分别与A连线,假设∠ACB=∠ADC=| π |
| 4 |
科目:高中数学 来源:不详 题型:单选题
| π |
| 4 |
| A.d<f<e | B.e<f<d | C.d=e<f | D.e=d>f |

科目:高中数学 来源:2007-2008学年湖北省武汉市华中师大一附中高三(上)期中数学试卷(文科)(解析版) 题型:选择题
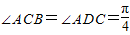 ,三角形ABC,ABD,ABE的外接圆直径分别为d,e,f,则( )
,三角形ABC,ABD,ABE的外接圆直径分别为d,e,f,则( )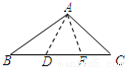
科目:高中数学 来源: 题型:单选题
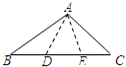 如图所示,在△ABC中,BC边上的两点D、E分别与A连线,假设
如图所示,在△ABC中,BC边上的两点D、E分别与A连线,假设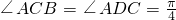 ,三角形ABC,ABD,ABE的外接圆直径分别为d,e,f,则
,三角形ABC,ABD,ABE的外接圆直径分别为d,e,f,则科目:高中数学 来源:不详 题型:解答题

科目:高中数学 来源: 题型:
 如图,在边长为12的正方形A1 AA′A1′中,点B、C在线段AA′上,且AB = 3,BC = 4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q;将该正方形沿BB1、CC1折叠,使得A′A1′ 与AA1重合,构成如图所示的三棱柱ABC—A1B1C1,在三棱柱ABC—A1B1C1中, (Ⅰ)求证:AB⊥平面BCC1B1; (Ⅱ)求面PQA与面ABC所成的锐二面角的大小.(Ⅲ)求面APQ将三棱柱ABC—A1B1C1分成上、下两部分几何体的体积之比.
如图,在边长为12的正方形A1 AA′A1′中,点B、C在线段AA′上,且AB = 3,BC = 4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q;将该正方形沿BB1、CC1折叠,使得A′A1′ 与AA1重合,构成如图所示的三棱柱ABC—A1B1C1,在三棱柱ABC—A1B1C1中, (Ⅰ)求证:AB⊥平面BCC1B1; (Ⅱ)求面PQA与面ABC所成的锐二面角的大小.(Ⅲ)求面APQ将三棱柱ABC—A1B1C1分成上、下两部分几何体的体积之比.
 | |||
 | |||
科目:高中数学 来源:江苏省盐城中学2010-2011学年高一下学期期中考试数学试题 题型:044
市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4万米,BC=6万米,CD=2万米.

(Ⅰ)求原棚户区建筑用地ABCD中对角A,C两点的距离;
(Ⅱ)请计算出原棚户区建筑用地ABCD的面积及圆的半径R;
(Ⅲ)因地理条件的限制,边界AD,DC不能变更,而边界AB,BC可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧ABC上设计一点P,使得棚户区改造的新建筑用地APCD的面积最大,并求最大值.
科目:高中数学 来源:2009年高考数学第二轮执点专题测试:立体几何(含详解) 题型:044
如图1所示,在边长为12的正方形![]() 中,点B、C在线段
中,点B、C在线段![]() 上,且AB=3,BC=4,作BB1∥AA1,分别交A1
上,且AB=3,BC=4,作BB1∥AA1,分别交A1![]() 、A
、A![]() 于点B1、P,作CC1∥AA1,分别交A1
于点B1、P,作CC1∥AA1,分别交A1![]() 、A
、A![]() 于点C1、Q,将该正方形沿BB1、CC1折叠,使得
于点C1、Q,将该正方形沿BB1、CC1折叠,使得![]() 与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
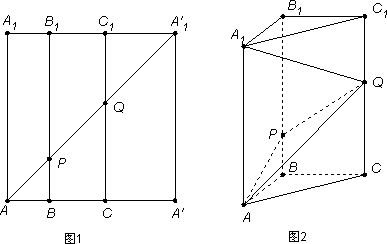
(Ⅰ)在三棱柱ABC-A1B1C1中,求证:AB⊥平面BCC1B1;
(Ⅱ)求平面APQ将三棱柱ABC-A1B1C1分成上、下两部分几何体的体积之比.
科目:高中数学 来源:湖南省郴州市一中2012届高三第六次质量检测数学理科试题 题型:044
如图(1)所示:在边长为12的正方形![]() 中,BB1∥CC1∥AA1,且AB=3,BC=4,
中,BB1∥CC1∥AA1,且AB=3,BC=4,![]() 分别交BB1、CC1于P、Q两点,将正方形沿BB1、CC1折叠,使得
分别交BB1、CC1于P、Q两点,将正方形沿BB1、CC1折叠,使得![]() 与AA1重合,构成如图(2)所示的三棱柱ABC-A1B1C1.
与AA1重合,构成如图(2)所示的三棱柱ABC-A1B1C1.

(Ⅰ)在底边AC上有一点M,且AM∶MC=3∶4,求证:BM∥平面APQ;
(Ⅱ)求直线BC与平面A1PQ所成角的正弦值.
科目:高中数学 来源: 题型:
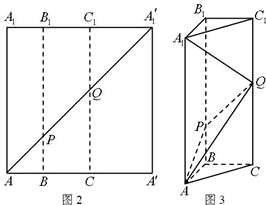 如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.
如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com