
科目:初中数学 来源:陕西 题型:单选题
A.AD>
| ||
B.AD=
| ||
C.AD<
| ||
| D.AD与AB+AC的大小关系不确定 |

科目:初中数学 来源:1997年陕西省中考数学试卷(解析版) 题型:选择题

 (AB+AC)
(AB+AC) (AB+AC)
(AB+AC)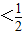 (AB+AC)
(AB+AC)科目:初中数学 来源: 题型:单选题
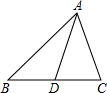 如图,已知在△ABC中,AD是BC边上的中线,则下列结论中正确的是
如图,已知在△ABC中,AD是BC边上的中线,则下列结论中正确的是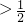 (AB+AC)
(AB+AC) (AB+AC)
(AB+AC)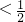 (AB+AC)
(AB+AC)科目:初中数学 来源: 题型:解答题
 如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是______
如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是______

科目:初中数学 来源: 题型:解答题
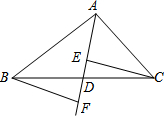 如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连结CE、BF.
如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连结CE、BF.科目:初中数学 来源:2012年北京市房山区中考数学二模试卷(解析版) 题型:解答题

科目:初中数学 来源: 题型:阅读理解
 24、先阅读下面的材料,然后解答问题:
24、先阅读下面的材料,然后解答问题: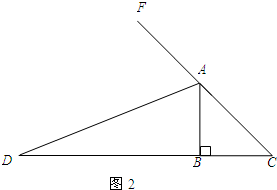
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com