
科目:初中数学 来源: 题型:
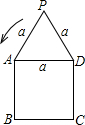 如图,等边三角形和正方形的边长都是a,在图形所在的平面内,将△PAD以点A为中心沿逆时针方向旋转,使AP与AB重合,如此继续分别以点B、C、D 为中心将三角形进行旋转,使点P回到原来位置为止,则点P从开始到结束所经过路径的长为( )
如图,等边三角形和正方形的边长都是a,在图形所在的平面内,将△PAD以点A为中心沿逆时针方向旋转,使AP与AB重合,如此继续分别以点B、C、D 为中心将三角形进行旋转,使点P回到原来位置为止,则点P从开始到结束所经过路径的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
科目:初中数学 来源:不详 题型:单选题
A.
| B.
| C.
| D.
|

科目:初中数学 来源: 题型:单选题
 如图,等边三角形和正方形的边长都是a,在图形所在的平面内,将△PAD以点A为中心沿逆时针方向旋转,使AP与AB重合,如此继续分别以点B、C、D 为中心将三角形进行旋转,使点P回到原来位置为止,则点P从开始到结束所经过路径的长为
如图,等边三角形和正方形的边长都是a,在图形所在的平面内,将△PAD以点A为中心沿逆时针方向旋转,使AP与AB重合,如此继续分别以点B、C、D 为中心将三角形进行旋转,使点P回到原来位置为止,则点P从开始到结束所经过路径的长为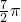 a
a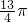 a
a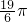 a
a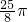 a
a科目:初中数学 来源: 题型:
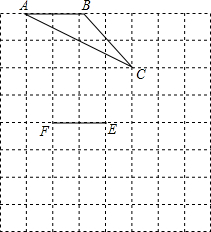 形的顶点上.
形的顶点上.科目:初中数学 来源: 题型:
| 3 |
| 1 |
| 6 |
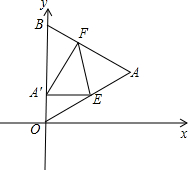 若能,请求出此时点A′的坐标;若不能,请你说明理由.
若能,请求出此时点A′的坐标;若不能,请你说明理由.科目:初中数学 来源: 题型:
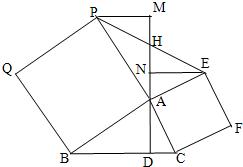 17、如图,以锐角△ABC的边AB、AC向外作正方形APQB和正方形AEFC,连接PE,作AD⊥BC,垂足为D,延长DA交PE于点H.过P作PM⊥DM,垂足为M,过点E作EN⊥DM,垂足为N.
17、如图,以锐角△ABC的边AB、AC向外作正方形APQB和正方形AEFC,连接PE,作AD⊥BC,垂足为D,延长DA交PE于点H.过P作PM⊥DM,垂足为M,过点E作EN⊥DM,垂足为N.科目:初中数学 来源: 题型:
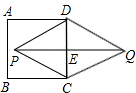 如图,正方形ABCD的边长为3,以CD为一边向CD两侧作等边三角形PCD和等边三角形QCD,那么PQ的长是( )
如图,正方形ABCD的边长为3,以CD为一边向CD两侧作等边三角形PCD和等边三角形QCD,那么PQ的长是( )A、
| ||||
B、
| ||||
C、3
| ||||
D、6
|
科目:初中数学 来源: 题型:
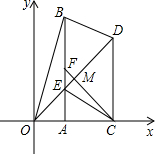 化时,Rt△OAB的面积恒为
化时,Rt△OAB的面积恒为| 1 | 2 |
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
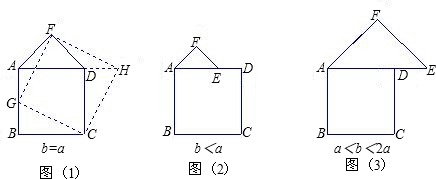
| BG | AE |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com