
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:单选题
下列说法:
①平行四边形对角线相等; ②平行四边形对角线的交点到一组对边的距离相等;
③一组对边相等,且有一组对角相等的四边形是平行四边形; ④旋转后能重合的两个图形是中心对称;
⑤对角线相等且互相垂直的四边形是正方形.
其中正确的个数有
科目:初中数学 来源:活学巧练八年级数学上 题型:013
下列说法:①平行四边形对角线相等;②平行四边形对角线的交点到一组对边的距离相等;③一组对边相等,且有一组对角相等的四边形是平行四边形;④旋转后能重合的两个图形是中心对称;⑤对角线相等且互相垂直的四边形是正方形.其中正确的个数有
[ ]
科目:初中数学 来源: 题型:
| 3 |
-
|
| ||
| a |
| A、4 | B、3 | C、2 | D、1 |
科目:初中数学 来源:黑龙江 题型:单选题
| 3 |
-
|
| ||
| a |
| A.4 | B.3 | C.2 | D.1 |
科目:初中数学 来源: 题型:单选题
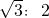 ,那么这两个三角形的面积之比是3:4
,那么这两个三角形的面积之比是3:4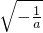 的化简结果是
的化简结果是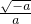 .
.科目:初中数学 来源:2002年全国中考数学试题汇编《圆》(01)(解析版) 题型:选择题
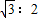 ,那么这两个三角形的面积之比是3:4
,那么这两个三角形的面积之比是3:4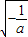 的化简结果是
的化简结果是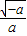 .
.科目:初中数学 来源:2002年全国中考数学试题汇编《四边形》(01)(解析版) 题型:选择题
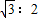 ,那么这两个三角形的面积之比是3:4
,那么这两个三角形的面积之比是3:4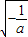 的化简结果是
的化简结果是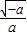 .
.科目:初中数学 来源:2002年全国中考数学试题汇编《二次根式》(01)(解析版) 题型:选择题
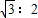 ,那么这两个三角形的面积之比是3:4
,那么这两个三角形的面积之比是3:4 的化简结果是
的化简结果是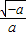 .
.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com