
科目:初中数学 来源:2012-2013学年北师大版九年级(上)期中数学试卷(1)(解析版) 题型:选择题
科目:初中数学 来源:模拟题 题型:解答题
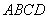 中,
中,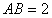 ,
,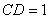 ,∠A=60°,∠B﹦∠D﹦90°, 求四边形
,∠A=60°,∠B﹦∠D﹦90°, 求四边形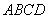 的面积;
的面积;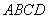 中,AB∥CD,CE是∠
中,AB∥CD,CE是∠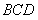 的平分线,且CE⊥AD,
的平分线,且CE⊥AD,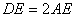 ,CE把梯形
,CE把梯形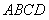 分成面积为
分成面积为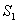 和S2的两部分,若
和S2的两部分,若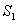 ﹦1,求
﹦1,求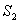 的值
的值
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
科目:初中数学 来源:2011年安徽省数学竞赛卷 题型:解答题
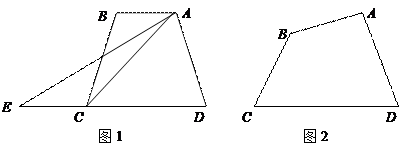
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.如,平行四边形的一条对角线所在的直线就是平行四边形的一条面积等分线.
(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的是_______;
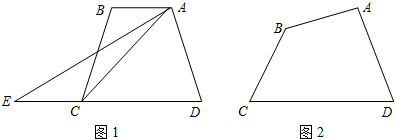
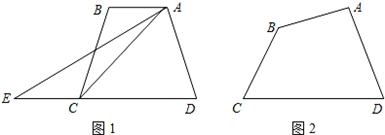
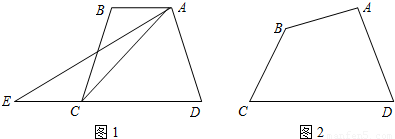
(2)如图1,梯形ABCD中,AB∥DC,如果延长DC到E,使CE=AB,连接AE,那么有S梯形ABCD =S△ADE.请你给出这个结论成立的理由,并过点A作出梯形ABCD的面积等分线(不写作法,保留作图痕迹);
(3)如图2,四边形ABCD中,AB与CD不平行,S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并给出说明;若不能,说明理由.

科目:初中数学 来源:江苏期中题 题型:解答题
科目:初中数学 来源:2010-2011学年江苏省无锡市江阴高级中学九年级(上)期中数学试卷(解析版) 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com