Question

11．毕达哥拉斯学派对”数”与”形”的巧妙结合作了如下研究：

名称及图形 几何点数 层数	三角形数	正方形数	五边形数	六边形数
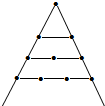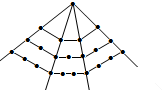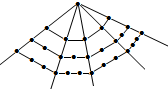第一层几何点数	1	1	1	1
第二层几何点数	2	3	4	5
第三层几何点数	3	5	7	9
…	…	…	…	…
第六层几何点数	6	11	16	21
…	…	…	…	…
第n层几何点数	n	2n-1	3n-2	4n-3

请写出第六层各个图形的几何点数，并归纳出第n层各个图形的几何点数．

Answer 1

分析 首先看三角形数，根据前三层的几何点数分别是1、2、3，可知第六层的几何点数是6，第n层的几何点数是n；然后看正方形数，根据前三层的几何点数分别是1=2×1-1，3=2×2-1，5=2×3-1，可知第六层的几何点数是2×6-1=11，可知第n层的几何点数是2n-1；再看五边形数，根据前三层的几何点数分别是1=3×1-2，4=3×2-1，7=3×3-2，可知第六层的几何点数是3×6-2=16，可知第n层的几何点数是3n-2；最后看六边形数，根据前三层的几何点数分别是1=4×1-3，5=4×2-3，9=4×3-3，可知第六层的几何点数是4×6-3=21，可知第n层的几何点数是4n-3；据此解答即可．

解答 解：因为：
前三层三角形数的几何点数分别是1、2、3，
所以：
第六层的几何点数是6，第n层的几何点数是n；
因为：
前三层的正方形几何点数分别是1=2×1-1，3=2×2-1，5=2×3-1，
所以：
第六层的几何点数是2×6-1=11，可知第n层的几何点数是2n-1；
因为：
前三层五边形的几何点数分别是1=3×1-2，4=3×2-1，7=3×3-2，
所以：
第六层的几何点数是3×6-2=16，可知第n层的几何点数是3n-2；
因为：
前三层六边形的几何点数分别是1=4×1-3，5=4×2-3，9=4×3-3，
可知第六层的几何点数是4×6-3=21，可知第n层的几何点数是4n-3．

名称及图形 几何点数 层数	三角形数	正方形数	五边形数	六边形数
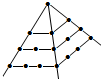第一层几何点数	1	1	1	1
第二层几何点数	2	3	4	5
第三层几何点数	3	5	7	9
…	…	…	…	…
第六层几何点数	6	11	16	21
…	…	…	…	…
第n层几何点数	n	2n-1	3n-2	4n-3

故答案为：6，11，16，21，n，2n-1.3n-2.4n-3．

点评 主要考查了学生通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．