Question

5．6个点最多可以连15条线段．

Answer 1

分析 求6个点最多可以连成多少条线段，实际是属于握手问题：由一个点向另外5个点可以连成5条线段，在不重复的情况下，第二个点可以连成4条线段，第三个点可以连成3条线段，第四个点可以连成2条线段，第五个点能连成1条线段．

解答 解：如图：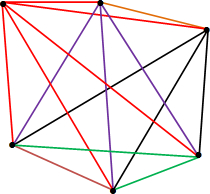

一共可以组成的线段条数是：
5+4+3+2+1=15（条）；
答：一共有15条．
故答案为：15．

点评 把点的个数看作n，即n个点，那么可连线段的总条数就等于从1开始前（n-1）个连续自然数的和．