
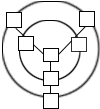
 将自然数1、10、19、28、37、46、55分别填入图中的七个框中,使每条直线上的三数之和与每个圆周上的三数之和都相等.那么圆心上的那个数应该填
将自然数1、10、19、28、37、46、55分别填入图中的七个框中,使每条直线上的三数之和与每个圆周上的三数之和都相等.那么圆心上的那个数应该填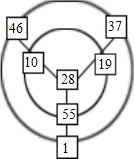


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:小学数学 来源: 题型:
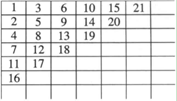 (2010?海安县)将自然数1,2,3,4…按如图那样的顺序排列起来.在最上面的一行中,从左到右第10个数是
(2010?海安县)将自然数1,2,3,4…按如图那样的顺序排列起来.在最上面的一行中,从左到右第10个数是查看答案和解析>>
科目:小学数学 来源: 题型:
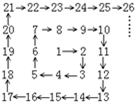 将自然数1,2,3,4…按箭头所指方向顺序排列(如图),依次在2,3,5,7,10…等数的位置处拐弯.
将自然数1,2,3,4…按箭头所指方向顺序排列(如图),依次在2,3,5,7,10…等数的位置处拐弯.查看答案和解析>>
科目:小学数学 来源: 题型:
查看答案和解析>>
科目:小学数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com