
 :x=2
:x=2 :1.8
:1.8 ]×(1÷
]×(1÷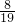 -2.375)]+2.901
-2.375)]+2.901 和原二班的
和原二班的 组成新一班,将原一班的
组成新一班,将原一班的 和原二班的
和原二班的 组成新二班,余下的30人组成新三班.如果新一班的人数比新二班的人数多10%.原一班有多少人?
组成新二班,余下的30人组成新三班.如果新一班的人数比新二班的人数多10%.原一班有多少人? :x=2
:x=2 :1.8
:1.8 x=
x= ×1.8,
×1.8, x=1,
x=1, x÷
x÷ =1÷
=1÷ ,
,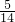 ;
; ]×(1÷
]×(1÷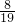 -2.375)]+2.901,
-2.375)]+2.901, -
- )=72(人);
)=72(人); -
- )=24(人);
)=24(人); ÷
÷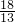 =
= ,
, -
- )=16÷
)=16÷ =16×
=16×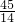 =51
=51 (千米);
(千米); 千米.
千米. x=
x= ×1.8,再根据等式的基本性质,方程的两边同时除以
×1.8,再根据等式的基本性质,方程的两边同时除以 来解;
来解; 和1÷
和1÷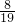 ,再算中括号里的1.4+3.6和2.375-2.375.最后算0+2.901;
,再算中括号里的1.4+3.6和2.375-2.375.最后算0+2.901;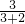 =
= ;则乙行了全程的
;则乙行了全程的 ;提速后,甲速:乙速=3(1+20%):2(1+30%)=18:13;同样在相同时间内,速度比等于路程比,乙行路程是甲行路程的
;提速后,甲速:乙速=3(1+20%):2(1+30%)=18:13;同样在相同时间内,速度比等于路程比,乙行路程是甲行路程的 ,当甲到达B地时,甲又行了全程的
,当甲到达B地时,甲又行了全程的 ,乙应该行了全程的
,乙应该行了全程的 ×
× =
= ,16千米就相当于全程的(
,16千米就相当于全程的( -
- ),用除法解答即可;
),用除法解答即可;

科目:小学数学 来源: 题型:
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
 :x=2
:x=2 :1.8
:1.8  )×(1÷
)×(1÷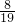 -2.375)]+2.901
-2.375)]+2.901 +
+ +
+ +
+ +…+
+…+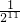 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com