Question

求图形阴影部分的面积

Answer 1

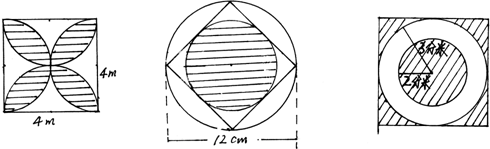
分析：（1）观察图形可知，边长4米的正方形的面积减去左右两个直径4米的半圆（即直径是4米的圆）的面积，就是2个空白处的面积，据此用正方形的面积减去4个空白处的面积即可解答，
（2）观察图形可知，阴影部分是一个圆，所以只要求出半径即可解答，圆的半径等于正方形的边长的一半，所以设圆的半径是r，则正方形的边长是2r；外部的圆的直径是12厘米，则内部的正方形的面积就是12×6÷2×2=72平方厘米，即2r×2r=72，所以可得r²=18，据此代入圆的面积公式计算即可解答．
（3）观察图形可知，用外部的正方形的面积减去中间圆环的面积，就是阴影部分的面积，由外圆的半径是3分米，可得出正方形的边长是3+3=6分米，据此即可解答．

解答：解：（1）4×4-3.14×(

4

2

)2，
=16-12.56，
=3.44（平方米），
16-3.44×2，
=16-6.88，
=9.12（平方米），
答：阴影部分的面积是9.12平方米．

（2）设圆的半径是r，则正方形的边长是2r；
外部的圆的直径是12厘米，则内部的正方形的面积就是12×6÷2×2=72平方厘米，
即2r×2r=72，所以可得r²=18，
所以圆的面积是：3.14×18=56.52（平方厘米），
答：阴影部分的面积是56.52平方厘米．

（3）正方形的边长是3×2=6（分米），
6×6-3.14×（3²-2²），
=36-15.7，
=20.3（平方分米），
答：阴影部分的面积是20.3平方分米．

点评：此题主要考查组合图形的面积的计算方法，要注意图形的等积变形．