
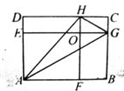
 如图,已知长方形HOGC,DEOH,OFBG,的面积比为1:2:3,若三角形AGH的面积为12平方厘米,求长方形ABCD的面积.
如图,已知长方形HOGC,DEOH,OFBG,的面积比为1:2:3,若三角形AGH的面积为12平方厘米,求长方形ABCD的面积.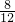 ×长方形ABCD面积;
×长方形ABCD面积;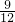 ×长方形ABCD面积;
×长方形ABCD面积; ×长方形ABCD面积;
×长方形ABCD面积; ×
×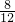 ×长方形ABCD面积=
×长方形ABCD面积= 长方形ABCD面积;
长方形ABCD面积; ×
×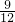 ×长方形ABCD面积=
×长方形ABCD面积= 长方形ABCD面积;
长方形ABCD面积; ×
× ×长方形ABCD面积=
×长方形ABCD面积= 长方形ABCD面积;
长方形ABCD面积; -
- -
- )×长方形ABCD面积=12,
)×长方形ABCD面积=12, ×长方形ABCD面积=12,
×长方形ABCD面积=12,

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com