解答:解:根据题意可得:
(1)根据竖式可得:E=1;
个位上:D+D的末尾还是0,只有0+0=0,所以D=0;
假设百位上向千位上进1,那么,A+1+1=10,A=8;
十位上:C+1=8,C=7;
百位上:B+B的末尾是7,没有两个相同的整数相加的末尾是7的数;
因此可以得出百位上相加的数的和没有满十;
千位上:A+1=10,A=10-1=9;
十位上:C+1=9,C=9-1=8;
百位上:B+B=8,B=4;
由以上推算可得竖式是:
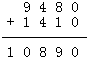
;
因此,A=9,B=4,B=8,D=0,E=1;
(2)根据竖式可得:A=1;
B-E不够减,上一位退1后想减得0,因为10-9=1,只有千位上向百位退1,这样才能得0;可得B=0,E=9;
十位上,0-1,不够减,百位上退1,10-1=9,与E=9重复,那么十位上必向个位上退1,这样9-1=8,可得:F=8;
百位上,C+1-1-8的末尾是8,8+8=16,可得:C=6;
个位上:10+D-G=8,G-D=2,数字不能重复;因此,G=4,D=2或G=5,D=3,或G=6,D=4;
由以上推算可得竖式是:

;
因此可得:A=1,B=0,C=7,D=2、3、4,E=9,F=8.
故答案为:9,4,8,0,1;1,0,7,2、3、4,9,8.

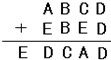

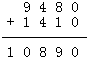 ;
; ;
;
