Question

如图中，ABCD是梯形，面积是1，已知

DF

FC

=

3

4

，

AE

EB

=

1

5

，

DC

AB

=

c

d

．问：

（1）三角形ECD的面积是多少？
（2）四边形EHFG的面积是多少？

Answer 1

考点：三角形面积与底的正比关系

专题：平面图形的认识与计算

分析：（1）设出梯形的高为h，即三角形的高，再利用梯形的面积公式和给出的梯形的面积，求出三角形的面积；
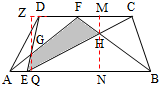
（2）过G作ZQ⊥AB与Q，交CD延长线与Z，过H作MN⊥AB与N，交DC与M，因为AB∥DC，所以QZ⊥DC，MN⊥DC，所以ZQ=MN=h，再利用相似三角形的对应边的比，分别求出积S_△DEC、S_△DGF、S_△FHC的面积，进而求出四边形EHFG的面积．

解答： 解：（1）设梯形ABCD的AB和CD之间的高是h，
则

DC

AB

=

c

d

所以AB=

d

c

DC
因为梯形ABCD的面积是1，
所以

1

2

（AB+CD）×h=1，

1

2

×（

d

c

DC+DC）×h=1，
所以DC×h=

2c

c+d

所以S_△ECD=

1

2

×DC×h=

1

2

×

2c

c+d

=

c

c+d

；
答：三角形ECD的面积是

c

c+d

．

（2）过G作ZQ⊥AB与Q，交CD延长线与Z，过H作MN⊥AB与N，交DC与M，
因为AB∥DC，
所以QZ⊥DC，MN⊥DC，
所以ZQ=MN=h，
因为

DF

CF

=

3

4

，

AE

BE

=

1

5

，AB=

d

c

DC，
所以DF=

3

7

DC，CF=

4

7

DC，
AE=

1

6

AB=

1

6

×

d

c

DC，BE=

5

6

×

d

c

DC=

5d

6c

DC，
因为DC∥AB，
所以△DGF∽△EGA，
所以

DF

AE

=

GZ

GQ

=

3DC 7

dDC 6

=

18c

7d

，
因为GZ+GQ=ZQ=h，
所以GZ=

18c

7d+18c

h，
所以S_△DGF=

1

2

×DF×GZ=

1

2

×

3

7

DC×

18c

7d+18c

CDh=

27c

7(18c+7d)

×

2c

c+d

=

54c2

7(18c+7d)(c+d)

同理：

CF

BE

=

HM

HN

=

4CD 7

5AB 6

=

4CD 7

5 6 × dCD c

=

24c

35d

，
所以HM=

24c

35d+24c

h，
所以S_△FHC=

1

2

×CF×HM=

1

2

×

4

7

CD×

24c

35d+24c

h=

48c

7(35d+24c)

×CDh=

48c

7(35d+24c)

×

2c

c+d

=

96c2

7(35d+24c)(c+d)

所以四边形EHFG的面积=S_△DEC-S_△DGF-S_△FHC=

c

c+d

-

54c2

7(18c+7d)(c+d)

-

96c2

7(35d+24c)(c+d)

=

3024c2d+1715d2c

7(18c+7d)(35d+24c)(c+d)

．
答：四边形EHFG的面积是

3024c2d+1715d2c

7(18c+7d)(35d+24c)(c+d)

．

点评：此题考查了三角形和梯形的面积公式即相似三角形的对应边的比相等．