
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 因为5194b是2的倍数,则b是偶数;又因为是3的倍数,所以满足:各个数位上数的和能被3整除,即:5+1+9+4+b=19+b是3的倍数,所以b=2,b=8;解答即可.
解答 解:由分析可知:b是偶数,并且:5+1+9+4+b=19+b是3的倍数,19+2=21,21能被3整除,19+8=27,27能被3整除,所以b=2,b=8都可以;
故选:A,D.
点评 解答此题应根据能同时被2和3整除的数的特征,进行解答即可.


科目:小学数学 来源: 题型:计算题
| 80+330= | 360÷12= | 765-60= | 130×7= |
| 520+90= | 910-280= | 25×40= | 7200÷80= |
| 297×8≈ | 503×21≈ | 590÷49≈ | 184÷60≈ |
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
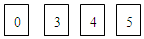
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com