Question

阴影面积是240，求三个正方形的面积？

Answer 1

考点：长方形、正方形的面积

专题：平面图形的认识与计算

分析：观察图可知：较大正方形的边长是较小正方形边长的2倍，如果设较小正方形的边长为x，那么较大正方形的边长就是2x；把边长是x+2x的正方形画完整，并用字母表示出各个顶点，再根据三角形的面积=底×高÷2，先分别求出△AEB、△ADC和△BFC的面积，再求出□ADFE的面积，进而用□ADFE的面积减去三个三角形面积的和就是阴影部分的面积，据此即可求得较小正方形的面积，进而求得三个正方形的面积和．

解答： 解：见下图：

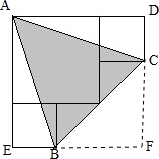
设较小正方形的边长为x，较大正方形的边长就是2x，最大正方形的边长为x+2x=3x
S△AEB=S△ADC=x×（x+2x）÷2=1.5x²
S△BFC=2x×2x÷2=2x²
S△AEB+S△ADCS+△BFC
=1.5x²+1.5x²+2x²
=5x²
S□ADFE=（3x）²=9x²
S△ABC=S□ADFE-（S△AEB+S△ADCS+△BFC）
=9x²-5x²
=4x²
因为S△ABC=240，所以4x²=240，那么x²=240÷4=60
所以三个正方形的面积和：
x²+（2x）²+x²=60+240+60=360．

点评：此题重点考查三角形和正方形面积计算公式的运用，解决此题关键是先求出三个空白三角形的面积，进而求出大正方形的面积，再根据阴影部分的面积，求得小正方形的面积，从而问题得解．