练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情

    哥尼斯堡七桥问题：俄国十八世纪的哥尼斯堡有七座桥，连接着两河交汇处的四个岛屿(如下图所示)．当时那里的人们热衷于这样一个话题：一个散步者，能否从一个岛屿出发，走遍所有的七座桥，而且不重复?你能回答这个问题吗?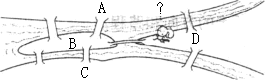

    答案：
    解析：

    　　如图所示，我们可以把岛屿抽象地看成4个点：A、B、C、D。各个岛屿之间有几座桥相连，我们就看作四点之间有几条线相连。这样，这个问题就抽象成一个一笔画问题。图中A、B、C、D四点均为奇点，所以此图不能一笔画出。即一个散步者，不能从一个岛屿出发，不重复地走遍所有的七座桥。


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：

    大西洋总面积约一亿零九十万三千零二平方千米，这个数写作
    100903002
    100903002
    ；太平洋总面积约178680000平方千米，这个数读作
    一亿七千八百六十八万
    一亿七千八百六十八万
    ，省略亿后面的尾数约是
    2
    2
    亿．

    查看答案和解析>>

    科目：小学数学 来源： 题型：阅读理解

    下面是我国第六次人口普查数据公布的部分内容，阅读并回答问题．
    根据《全国人口普查条例》和《国务院关于开展第六次全国人口普查的通知》，我国以2010年11月1日零时为标准时点进行了第六次全国人口普查．在国务院和地方各级人民政府的统一领导下，在全体普查对象的支持配合下，通过广大普查工作人员的艰苦努力，目前已圆满完成人口普查任务．现将快速汇总的主要数据公布如下：
    全国总人口为
    1339724852
    1339724852
    人．其中：
    普查登记的大陆31个省、自治区、直辖市和现役军人的人口共1339724852
    十三亿三千九百七十二万四千八百五十二
    十三亿三千九百七十二万四千八百五十二
    人，同第五次全国人口普查2000年11月1日零时的1265825048
    十二亿六千五百八十二万五千零四十八
    十二亿六千五百八十二万五千零四十八
    人相比，十年共增加73899804
    七千三百八十九万九千八百零四
    七千三百八十九万九千八百零四
    人．
    香港特别行政区人口为7097600
    七百零九万七千六百
    七百零九万七千六百
    人．
    澳门特别行政区人口为552300
    五十五万二千三百
    五十五万二千三百
    人．
    台湾地区人口为23162123
    二千三百一十六万二千一百二十三
    二千三百一十六万二千一百二十三
    人．
    （ 1）读出上面短文中的数
    （2）将上面各数超过1亿的改写为以亿为单位的近似数，不足1亿的改写为以万为单位的近似数
    13亿，13亿，7390万，710万，55万，2316万
    13亿，13亿，7390万，710万，55万，2316万
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    七座桥的故事
    在一个城市中有七座桥和四个区域，人们长期来往于七座桥之间．有人提出这样一个问题：能不能一次走遍所有的七座桥，而每座桥只准经过一次？问题提出后，很多人对此很感兴趣，纷纷进行试验，但在相当长的时间里，始终未能解决．最后，人们只好把这个问题向一个数学家提出，请他帮助解决．
    数学家接到了“七桥问题’’，连试了好几种走法都不行．好家伙，这样一种方法一种方法地试下去，要试到哪一天才能得出答案呢？他想：不能这样呆笨地试下去，得想别的方法．
    聪明的数学家终于想出一个巧妙的办法．他用“1、2、3、4、5、6、7”表示七座桥，它们连接着A、B、C、D四个区域（如图所示）．这样一来，七座桥的问题，就转变为数学分支“图论”中的一个一笔画问题，即能不能一笔从头到尾不重复地画出这个图形．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    34.7%读作：
    百分之三十四点七
    百分之三十四点七
    ，百分之一百二十写作：
    120%
    120%
    ．

    查看答案和解析>>

    同步练习册答案