考点:组合图形的面积
专题:平面图形的认识与计算
分析:设圆的半径为r,取AD的中点G,过G作EF的垂线交EF与O,连接EG、FG,则有
r2=()2+()2=,因为EO=OG,FO=OG,所以∠EGO=45°,∠FGO=45°,∠EGF=90°,因此阴影部分的面积等于扇形的面积减去三角形EFG的面积,然后再乘以2,据此解答即可.
解答:
解:设圆的半径为r,取AD的中点G,过G作EF的垂线交EF与O,连接EG、FG,
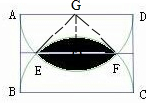
则有
r2=()2+()2=,
因为EO=OG,FO=OG,
所以∠EGO=45°,∠FGO=45°,∠EGF=90°,
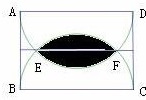
因此阴影部分的面积等于扇形的面积减去三角形EFG的面积,然后再乘以2,
则阴影部分面积为:
(3.14×
×-3×
÷2)×2
=(3.5325-2.25)×2
=1.2825×2
=2.565
答:阴影部分的面积是2.565.
点评:此题主要考查了组合图形的面积的求法,解答此题的关键是熟练掌握扇形和三角形的面积公式.




 阅读快车系列答案
阅读快车系列答案