Question

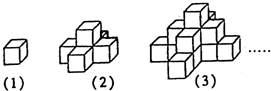
10．图（1）是一个水平摆放的小正方体木块，图（2）、（3）是由这样的小正方体木块叠放而成的．按照这样的规律继续叠放下去，第七个图形中，小正方体木块总数应是91．

Answer 1

分析 图（1）中只有一层，有（4×0+1）一个正方形，图（2）中有两层，在图（1）的基础上增加了一层，第二层有（4×1+1）个．图（3）中有三层，在图（2）的基础上增加了一层，第三层有（4×2+1），依此类推当图形有七层时总的正方体的个数．

解答 解：当图形有七层时，最下面一层的个数为：（4×6+1），
则此时总的正方体个数为：
1+（4×1+1）+（4×2+1）+（4×3+1）+（4×4+1）+（4×5+1）+（4×6+1）
=1+5+9+13+17+21+25
=（1+25）×7÷2
=26×7÷2
=13×7
=91
答：第七个图形中，小正方体木块总数应是91．
故答案为：91．

点评 本题考查了规律型：图形的变化．解题关键是根据图形的变换总结规律，由图形变换得规律：每次都比上一次增加一层，增加第n层时小正方形共增加了4（n-1）+1个，将n层的小正方形个数相加即可得到总的小正方形个数．