
分析 把C扇形的面积看作单位“1”,则B扇形的面积就是(1-$\frac{1}{4}$),再把B扇形的面积看作单位“1”,则A扇形的面积就是(1-$\frac{1}{4}$)×(1-$\frac{1}{3}$),求出A、B、C三个扇形的面积之比,再把比转化成分数,用圆周角的度数(360°)乘最小的扇形的圆心角度数所占的分率就是就是最小的扇形的圆心角的度数.
解答 解:设扇形C的面积为:“1”
则扇形B的面积为:1-$\frac{1}{4}$=$\frac{3}{4}$
扇形A的面积为:$\frac{3}{4}$×(1-$\frac{1}{3}$)
=$\frac{3}{4}$×$\frac{2}{3}$
=$\frac{1}{2}$
扇形A、B、C面积的比是:$\frac{1}{2}$:$\frac{3}{4}$:1=2:3:4
360°×$\frac{2}{2+3+4}$
=360°×$\frac{2}{9}$
=80°
答:面积最小的扇形的圆心角是80度.
故答案为:80.
点评 解答此题的关键是求出三个扇形面积的比,再把比转化成分数,然后根据分数乘法的意义,用360°乘最小的扇形所占的分率.


科目:小学数学 来源: 题型:填空题
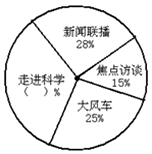 如图是某学校教师喜欢看的电视节目统计图,根据统计图回答问题.
如图是某学校教师喜欢看的电视节目统计图,根据统计图回答问题.查看答案和解析>>
科目:小学数学 来源: 题型:计算题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com