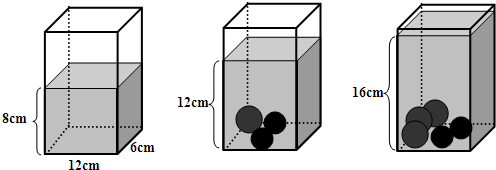
分析:(1)观察图形可知,长方体容器内原来水的高度是8厘米,放入一个大球两个小球后,水面上升到12厘米处,则三个球的体积就是上升部分水的体积:12×6×(12-8)=288立方厘米,
(2)再放入两个大球后水面又上升到16厘米,那么两个大球的体积就是这次上升的水的体积:12×6×(16-12)=288立方厘米,由此可得:一个大球的体积是:288÷2=144立方厘米,把这个大球的体积代入第一次放入的三个球中,即可求出一个小球的体积.
解答:解:12×6×(12-8),
=72×4,
=288(立方厘米);
1个大球的体积:12×6×(16-12)÷2,
=72×4÷2,
=144(立方厘米);
1个小球的体积是:(288-144)÷2,
=144÷2,
=72(立方厘米),
答:一个答圆球的体积是144立方厘米,小圆球的体积是72立方厘米.
点评:此题考查了长方体的体积公式的计算应用,关键是抓住上升部分的水的体积,分别求出两次放入水中的大球得体积.