
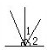
 两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的“夹角”(如图).如果在平面上画L条直线,要求它们两两相交,并且“夹角”只能是15°、30°、45°、60°、75°、90°之一,问:
两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的“夹角”(如图).如果在平面上画L条直线,要求它们两两相交,并且“夹角”只能是15°、30°、45°、60°、75°、90°之一,问:

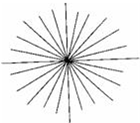 的“夹角”和是:
的“夹角”和是:

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:小学数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com