
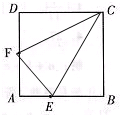
 如图,正方形ABCD的边长为8厘米,E,F是边上的两点,且AE=3厘米,AF=4厘米,在正方形的边界上再选一点P,使得三角形EFP的面积尽可能大,这个面积的最大值是________平方厘米.(在图上画出三角形)
如图,正方形ABCD的边长为8厘米,E,F是边上的两点,且AE=3厘米,AF=4厘米,在正方形的边界上再选一点P,使得三角形EFP的面积尽可能大,这个面积的最大值是________平方厘米.(在图上画出三角形) ×EF×h
×EF×h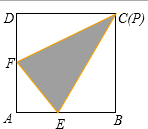


 阅读快车系列答案
阅读快车系列答案科目:小学数学 来源: 题型:
 如图中正方形ABCD是一条环形公路.已主口汽车在AB上时速是90千米,在BC上的时速是120千米,在CD上的时速是60千米,在DA上的时速是80 千米,从CD上一点P,同时反向各发出一辆汽车,它们将在AB中点相遇,如果从PC的中点M同时反向各发出一辆汽车,它们将在AB上-点N相遇,那么
如图中正方形ABCD是一条环形公路.已主口汽车在AB上时速是90千米,在BC上的时速是120千米,在CD上的时速是60千米,在DA上的时速是80 千米,从CD上一点P,同时反向各发出一辆汽车,它们将在AB中点相遇,如果从PC的中点M同时反向各发出一辆汽车,它们将在AB上-点N相遇,那么| A至N的距离 | N至B的距离 |
查看答案和解析>>
科目:小学数学 来源: 题型:
 如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是
如图,正方形ABCD的边长为12,P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是查看答案和解析>>
科目:小学数学 来源: 题型:
 如图,正方形ABCD的边长是4厘米,BD是对角线,BC、CD的中点分别是E、F,连接EF,EF的中点时I,AI与BD的交点是G,BG、DG的中点分别是H、J,连接EH、IJ,分别用甲、乙、丙、丁、戊、己、庚表示7个图形.
如图,正方形ABCD的边长是4厘米,BD是对角线,BC、CD的中点分别是E、F,连接EF,EF的中点时I,AI与BD的交点是G,BG、DG的中点分别是H、J,连接EH、IJ,分别用甲、乙、丙、丁、戊、己、庚表示7个图形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com