Question

【题目】三角形ABE，四边形AECF，三角形AFD的面积相等．求三角形AEF的面积．（单位：米）

Answer 1

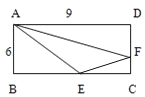
【答案】15平方米

【解析】

试题分析：根据长方形的面积公式S=ab，求出长方形ABCD的面积，再除以3就是三角形ABE，四边形AECF，三角形AFD的面积，再求出BE与DF的长度，进而求出EC与CF的长度，继而求出三角形EFC的面积，最后求出三角形AEF的面积．

解：三角形ABE，四边形AECF，三角形AFD的面积：6×9÷3=18（平方米），

BE的长度：18×2÷6=6（米），

DF的长度：18×2÷9=4（米），

三角形EFC的面积：（9﹣6）×（6﹣4）÷2，

=3×2÷2，

=3（平方米），

三角形AEF的面积：18﹣3=15（平方米），

答：三角形AEF的面积是15平方米．