
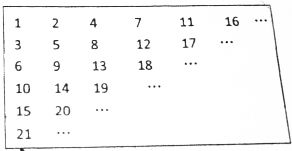
分析 从右上到左下可以看成这样的数列:
1,
2、3,
4、5、6,
7、8、9、10,
11、12、13、14、15,
…
每组有的数字个数分别是1,2,3,4,…
1679所在的组数满足这样的条件:
n(n+1)÷2≤1679,找出n的最大值,并求出1679所在的位置;根据1679在这组数中的位置求解.
解答 解:从右上到左下这一条斜线上的数可以看成一组数列,1679所在的组数满足:
n(n+1)÷2≤1679,
最大整数n=57,1679在第58组,前57组共有数:
1+2+3+…+57=1653,
1679-1653=26,1679排在第58条斜线上第26个位置上,即它处在26行上,
58-26+1=33,它处在33列上.
故答案为:26,33.
点评 本题不能按照图上直接给出的每行每列的思维找规律,需要通过斜线方向上找出规律,再根据规律求解.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com