


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:小学数学 来源: 题型:
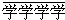 ”与“
”与“ ”的积是一个七位数,且它的个位和百万位数字与“学”所代表的数字相同,那么“
”的积是一个七位数,且它的个位和百万位数字与“学”所代表的数字相同,那么“ ”所能代表的两位数共有
”所能代表的两位数共有查看答案和解析>>
科目:小学数学 来源: 题型:
 有8个棱长为1cm的正方体(如图),3面是黑色,另3面是白色.现在,将颜色相同的面接合,组成一个棱长为2cm的大正方体.请问:有多少种符合要求的接合方式?(翻转后重合的也分别算不同的一种).
有8个棱长为1cm的正方体(如图),3面是黑色,另3面是白色.现在,将颜色相同的面接合,组成一个棱长为2cm的大正方体.请问:有多少种符合要求的接合方式?(翻转后重合的也分别算不同的一种).查看答案和解析>>
科目:小学数学 来源: 题型:
查看答案和解析>>
科目:小学数学 来源: 题型:
 右图是一个奥林匹克五环标识.这五个环相交成9部分A、B、C、D、E、F、G、H、I.请将数字1、2、3、4、5、6、7、8、9分别填入这9个部分中,使得五个环内的数字和恰好构成五个连续的自然数.问:这五个连续自然数的和的最大值是多少?
右图是一个奥林匹克五环标识.这五个环相交成9部分A、B、C、D、E、F、G、H、I.请将数字1、2、3、4、5、6、7、8、9分别填入这9个部分中,使得五个环内的数字和恰好构成五个连续的自然数.问:这五个连续自然数的和的最大值是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com