考点:组合图形的面积
专题:平面图形的认识与计算
分析:(1)用三角形的面积加上半圆的面积即可,三角形的高为圆的半径,底为圆的直径.
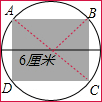
(2)如图,阴影部分是一个长方形,可分成两个直角三角形,每个三角形的高为圆的半径,底为圆的直径,运用三角形面积公式,即可解答.
(3)用正方形的面积减去圆的面积即可.
(4)阴影部分的面积=(大圆的面积-小圆的面积)÷2,小圆的半径为:6÷2=3(厘米),大圆的半径为:3+1=4(厘米),根据公式计算即可.
解答:
解:(1)16×(16÷2)÷2+3.14×(16÷2)2÷2
=16×8÷2+3.14×64÷2
=64+100.48
=164.48(平方厘米)
答:阴影部分的面积是164.48平方厘米.
(2)6×(6÷2)÷2×2
=6×3÷2×2
=18(平方厘米)
答:阴影部分的面积是18平方厘米.
(3)10×10-3.14×(10÷2)2
=100-3.14×25
=100-78.5
=21.5(平方厘米)
答:阴影部分的面积是21.5平方厘米.
(4)小圆的半径为:6÷2=3(厘米)
大圆的半径为:3+1=4(厘米)
(3.14×42-3.14×32)÷2
=3.14×(42-32)÷2
=3.14×(16-9)÷2
=3.14×7÷2
=10.99(平方厘米).
答:阴影面积为10.99平方厘米.
点评:关键是根据给出的图,找出阴影部分的面积在哪些学过的图形里面,再利用相应的公式解决问题.





 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案