
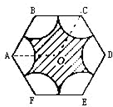
 如图所示,求阴影面积,图中是一个正六边形,面积为1040平方厘米,空白部分是6个半径为10厘米的小扇形.
如图所示,求阴影面积,图中是一个正六边形,面积为1040平方厘米,空白部分是6个半径为10厘米的小扇形.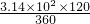 ,
,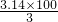 ,
, 可求得,为此需要知道半径和扇形弧的度数,由已知正六边形每边所对圆心角为60°,那么∠AOC=120°,又知四边形ABCD是平行四边形,所以∠ABC=120°,这样就能求出扇形的面积.从而可以求得阴影部分的面积.
可求得,为此需要知道半径和扇形弧的度数,由已知正六边形每边所对圆心角为60°,那么∠AOC=120°,又知四边形ABCD是平行四边形,所以∠ABC=120°,这样就能求出扇形的面积.从而可以求得阴影部分的面积.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com