
分析 把27盒饼干平均分成三份,每份9盒饼干,任取两份,分别放在天平秤两端,若平衡,则质量较轻的那瓶在未取的9盒饼干中,若不平衡;把天平秤较高端的9盒饼干平均分成三份,把其中的两份分别放在天平秤两端,若平衡,则质量较轻的那盒在未取的3盒饼干中,若不平衡,从较高端的3盒饼干中任取2盒饼干,分别放在天平秤两端即可解答.
解答 解:第一次:把27盒饼干平均分成三份,每份9盒饼干,任取两份,分别放在天平秤两端,若平衡,则质量较轻的那盒在未取的9盒饼干中(按照下面方法操作),若不平衡;
第二次:把天平秤较高端的9盒饼干平均分成三份,把其中两份分别放在天平秤两端,若天平秤平衡,则质量较轻的那瓶在未取的3盒饼干中(按照下面方法操作),若不平衡;
第三次:从较高端的3盒饼干中任取2盒饼干,分别放在天平秤两端,若天平秤平衡,则未取那盒饼干即为质量较轻的,若不平衡,则较高端的即为在质量较轻的.
所以,至少称3次就能保证找出质量较轻的饼干.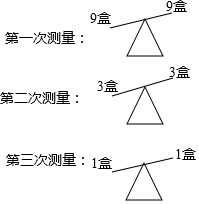
答:用天平秤至少称3次才能保证找到轻一些的饼干.
点评 本题主要考查学生依据天平秤平衡原理解决问题的能力.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
 |  |  |  |
| 14.2元 | 7.8元 | 30.6元 | 5.4元 |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:计算题
| $\frac{8}{21}$÷$\frac{5}{7}$ | $\frac{1}{5}$÷$\frac{4}{7}$ | 24÷$\frac{8}{21}$ |
| $\frac{3}{20}$÷$\frac{3}{4}$÷$\frac{2}{7}$ | 6×$\frac{5}{8}$÷$\frac{15}{4}$ | $\frac{1}{20}$÷$\frac{3}{4}$×$\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com