Question

求出如图阴影部分的周长和面积（单位：分米）

Answer 1

考点：组合图形的面积

专题：平面图形的认识与计算

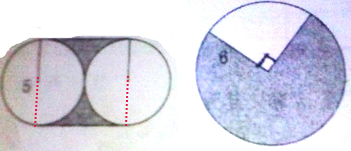
分析：如图所示：（1）阴影部分的周长就等于圆的周长，再加上圆的两条直径的长度，据此利用圆的周长=2πr即可求解；阴影部分的面积=正方形的面积-圆的面积，利用正方形和圆的面积公式即可求解．
（2）阴影部分的周长=圆的周长的

3

4

，再加上两条半径的长度；阴影部分的面积=圆的面积×

3

4

，据此解答即可．

解答： 解：（1）3.14×5×2+2×5×2
=31.4+20
=51.4（分米）
（5×2）×（5×2）-3.14×5²
=10×10-3.14×25
=100-78.5
=21.5（平方分米）
答：阴影部分的周长是51.4分米，面积是21.5平方分米．

（2）3.14×6×2×

3

4

+6×2
=28.26+12
=40.26（分米）
3.14×6²×

3

4

=3.14×36×

3

4

=3.14×27
=84.78（平方分米）
答：阴影部分的周长是40.26分米，面积是84.78平方分米．

点评：解答此题的关键是：弄清楚阴影部分的周长由哪些线段或曲线组成，阴影部分的面积可以由哪些图形的面积和或差求解．