在五(1)班举行的联欢会上,同学们通过抽签决定表演节目的形式,一共做了20张表演唱歌的签、12张表演朗诵的签、8张表演舞蹈的签.
(1)第一次抽签,表演唱歌的可能性是______,表演朗诵的可能性是______,表演舞蹈的可能性是______.
(2)节目进行到一半,已经有9人表演唱歌、6人表演朗诵、5人表演舞蹈.这时第21个人小东抽签,
表演唱歌的可能性是______,表演朗诵的可能性是______,表演舞蹈的可能性是______.
解:20+12+8=40(张),40÷2=20(张),
(1)表演唱歌:20÷40=

,
表演朗诵:12÷40=

,
表演舞蹈:8÷40=

,
答:第一次抽签,表演唱歌的可能性是

,表演朗诵的可能性是

,表演舞蹈的可能性是

.
(2)表演唱歌:(20-9)÷20=
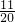
,
表演朗诵:(12-6)÷20=

,
表演舞蹈:(8-5)÷20=

,
答:表演唱歌的可能性是
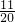
,表演朗诵的可能性是

,表演舞蹈的可能性是

.
故答案为:

,

,

,
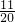
,

,

.
分析:(1)先求出第一次抽签的总张数:20+12+8=40(张),求抽到表演唱歌、表演朗诵、表演舞蹈的可能性,就相当于求20(或12或8)是40的几分之几,用除法计算,据此解答.
(2)先求出第二次抽签后剩余三种签的张数:表演唱歌的张数:20-9=11张,表演朗诵的张数:16-6=6张,表演舞蹈的张数:8-5=3张;求抽到表演唱歌、表演朗诵、表演舞蹈的可能性,就相当于求11(或6或3)是20的几分之几,用除法计算,据此解答.
点评:本题考查了简单事件发生的可能性的求解,即用可能性=所求情况数÷总情况数或求一个数是另一个数的几分之几用除法计算.

 ,
, ,
, ,
, ,表演朗诵的可能性是
,表演朗诵的可能性是 ,表演舞蹈的可能性是
,表演舞蹈的可能性是 .
.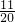 ,
, ,
, ,
,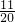 ,表演朗诵的可能性是
,表演朗诵的可能性是 ,表演舞蹈的可能性是
,表演舞蹈的可能性是 .
. ,
, ,
, ,
,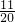 ,
, ,
, .
.
