Question

如图中共有

 

个正方体．

Answer 1

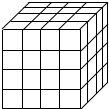
考点：组合图形的计数

专题：立体图形的认识与计算

分析：①1×1×1的小正方体：每条棱长上都是4个小正方体，所以利用正方体的体积公式计算，即可求出小正方体的总个数；
②2×2×2的正方体：每条棱上都可以3组，求出2×2×2正方体的总个数；
③3×3×3的正方体：每条棱上都可以3组，求出3×3×3正方体的总个数；
④4×4×4的正方体有1个；
把这些正方体的个数相加即可求解．

解答： 解：①最小的正方体：4×4×4=64（个）
②2×2×2的正方体：每条棱上都可以3组，
3×3×3=27（个）；
③3×3×3的正方体：每条棱上都可以3组，
3×3×3=27（个）；
④4×4×4的正方体有1个；
64+27+27+1=119（个）
答：共有 119个正方体．
故答案为：119．

点评：此题注意分类讨论，然后相加即可．