
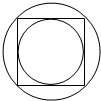
分析 设正方形的边长为1,则内圆的半径为$\frac{1}{2}$,外圆的半径为$\frac{\sqrt{2}}{2}$,由此即可求出内、外圆的面积,用外圆面积除以内圆面积.
解答 解:设正方形的边长为1
则内圆的半径为$\frac{1}{2}$,面积为π×($\frac{1}{2}$)2=$\frac{π}{4}$
外圆的半径为$\frac{\sqrt{2}}{2}$,面积为π×($\frac{\sqrt{2}}{2}$)2=$\frac{π}{2}$
$\frac{π}{2}$÷$\frac{π}{4}$=2
答:一个正方形的外接圆的面积是它的内接圆的2倍.
故答案为:2.
点评 此题单独求两个圆的面积不好求,这两个圆都与这个正方形有关系,可设这个正方形的边长为1,求出这两个圆的面积,进而求出外接圆的面积是它的内接圆的多少倍.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:小学数学 来源: 题型:解答题
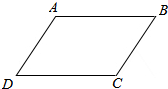 如图,两只蚂蚁从A点出发,大蚂蚁从A点经D点爬向C点,小蚂蚁从A点经过B点爬向C点,大蚂蚁每分钟爬30厘米,爬了5分钟到达C点,小蚂蚁用了6分钟到达C点.小蚂蚁平均每分钟爬了多少厘米?
如图,两只蚂蚁从A点出发,大蚂蚁从A点经D点爬向C点,小蚂蚁从A点经过B点爬向C点,大蚂蚁每分钟爬30厘米,爬了5分钟到达C点,小蚂蚁用了6分钟到达C点.小蚂蚁平均每分钟爬了多少厘米?查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
| 650÷50= | 25×4= | 1000÷125= |
| 1.26×1000= | 6.6÷100= | 450-200= |
| 37+68×0= | 56×78×0= | 523+497= |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com