
【题目】如图,长方形ABCD中,EF∥AD,GH∥AB,EF和GH相较于点O,长方形OFCH的面积比长方形AEOG的面积大6平方厘米,求三角形OBD的面积.
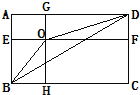
【答案】3平方厘米
【解析】
试题分析:如下图:因为S四边形BODC=S△BCD+S△BOD,
S阴影=S△ABD﹣S△BOD,
可以得出:2S△OBD=S四边形BODC﹣S四边形ABOD,
=(S△OBH+S长方形OFCH+S△OFD)﹣(S△OBE+S长方形AEOG+S△OGD),
=S长方形OFCH﹣S长方形AEOG,=6.
由此得出S△OBD的面积.
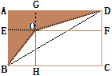
解:如图:
因为S四边形BODC=S△BCD+S△BOD,
S阴影=S△ABD﹣S△BOD,
可以得出:2S△OBD=S四边形BODC﹣S四边形ABOD,
=(S△OBH+S长方形OFCH+S△OFD)﹣(S△OBE+S长方形AEOG+S△OGD),
=S长方形OFCH﹣S长方形AEOG,=6(平方厘米),
所以 S△OBD=6÷2=3(平方厘米);
答:求三角形OBD的面积是3平方厘米.


 习题精选系列答案
习题精选系列答案科目:小学数学 来源: 题型:
【题目】
各式中的 表示什么数?
(1)193+ =325 (2)72× =216
(3) ﹣82=118 (4) ×45=405
(5)26.35+ =60.58 (6)96÷ =8
(7)![]() ﹣ =
﹣ =![]() (8)
(8)![]() + =
+ =![]()
(9)5+ =2×8 (10)9× =54÷2
(11) +26=65﹣22 (12)5× =80+÷2
(13 + =36 (14) × =81.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com