解:连接OC,OB,如上图所示
因为AB与小圆相切,所以OC⊥AB,
又因C为AB的中点,又AB=10,
所以AC=BC=

AB=5,
在直角三角形OAC中,
根据勾股定理得:OA
2=OC
2+AC
2=OC
2+25,
所以OA
2-OC
2=25,
则图中阴影部分面积为:
S=πOA
2-πOC
2,
=(OA
2-OC
2)π,
=25π,
=78.5(平方厘米);
答:阴影部分的面积是78.5平方厘米.
分析:如图所示,连接OC,OA,由大圆的弦AB与小圆相切,根据切线的性质得到OC垂直于AB,再由垂径定理得到C为AB的中点,由AB的长,求出AC的长,在直角三角形OAC中,根据勾股定理列出关系式,将AC的长代入求出OA
2-OC
2的长,由阴影部分为圆环形,根据大圆的面积减去小圆的面积可求出,表示出圆环的面积,将OA
2-OC
2的值代入即可求出圆环的面积,即为阴影部分的面积.
点评:此题考查了切线的性质,勾股定理,垂径定理,以及圆环面积的求法,利用了数形结合及整体代入的思想,熟练掌握切线的性质是解本题的关键.

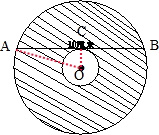
 如图,在两个同心圆上有一条两端点都在大圆上的切线与小圆相切,其长度为10厘米.求阴影部分的面积.(π取3.14)
如图,在两个同心圆上有一条两端点都在大圆上的切线与小圆相切,其长度为10厘米.求阴影部分的面积.(π取3.14) AB=5,
AB=5,

