解:(1)99999×22222+33333×33334,
=33333×3×22222+33333×33334,
=33333×(66666+33334)
=33333×100000,
=3333300000;
(2)2003×2004÷2004×2004-2003×2004,
=2003×2004-2003×2004,
=0;
(3)2.8×(

+
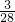
),
=2.8×

+2.8×
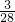
,
=0.4+0.3,
=0.7;
(4)101×
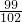
,
=(102-1)×
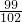
,
=102×
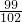
-1×
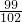
,
=99-
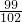
,
=98
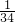
;
(5)9.81×10%+0.5×98.1+0.049×981,
=9.81×0.1+5×9.81+4.9×9.81,
=9.81×(0.1+5+4.9),
=9.81×10,
=98.1;
(6)23×
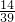
+14×
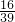
,
=23×
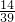
+16×
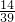
,
=(23+16)×
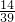
,
=39×
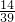
,
=14.
分析:(1)把99999看作33333×3,运用乘法分配律简算;
(2)先计算2004÷2004,原式变为2003×2004-2003×2004,故结果为0;
(3)运用乘法分配律简算;
(4)把101看作102-1,运用乘法分配律简算;
(5)先把原式变为9.81×0.1+5×9.81+4.9×9.81,运用乘法分配律简算;
(6)先把原式变为23×
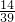
+16×
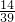
,运用乘法分配律简算.
点评:此题主要考查了学生对乘法分配律的灵活运用,以及改变运算顺序使计算简便.

 +
+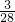 )
)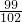
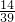 +14×
+14×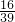 .
. +
+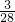 ),
), +2.8×
+2.8×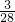 ,
,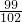 ,
,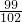 ,
,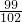 -1×
-1×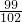 ,
,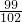 ,
,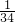 ;
;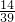 +14×
+14×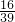 ,
,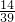 +16×
+16×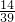 ,
,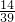 ,
,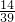 ,
,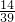 +16×
+16×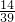 ,运用乘法分配律简算.
,运用乘法分配律简算.

 阅读快车系列答案
阅读快车系列答案