Question

7．如图，已知OC⊥AB，OD⊥OE，图中相等的角有∠BOE=∠COD，∠COE=∠AOD．

Answer 1

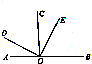
分析 根据垂直的定义可知，∠AOC=∠BOC=∠DOE=90°，因此∠AOD+∠COD=∠COE+∠COD=90°，由等式的性质可得，∠COE=∠AOD；同理可以得到∠BOE=∠COD；据此得解．

解答 解：因为OC⊥AB，OD⊥OE，
所以∠AOC=∠BOC=∠DOE=90°，
即∠AOD+∠COD=∠COE+∠COD=90°，
所以∠COE=∠AOD；
同理，由∠BOE+∠COE=∠COD+∠COE=90°，
可得∠BOE=∠COD．
故答案为：∠COD，∠AOD．

点评 本题考查了线段与角的综合，关键是能熟练掌握垂直的定义以及等式的性质．