Question

下面各涂色部分的面积．（单位：dm）

Answer 1

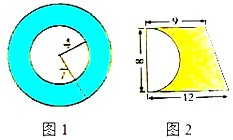
分析：（1）图1涂色部分的面积，根据圆环的面积的面积公式：S=π（R²-r²），列式计算即可求解；
（2）图2涂色部分的面积=梯形的面积-半圆的面积，列式计算即可求解．

解答：解：（1）图1涂色部分的面积：
3.14×（7²-4²），
=3.14×（49-16），
=3.14×33，
=103.62（dm²）；

（2）图2涂色部分的面积：
（9+12）×8÷2-3.14×（8÷2）²÷2，
=21×8÷2-3.14×16÷2，
=84-25.12，
=58.88（dm²）．
答：图1涂色部分的面积是103.62dm²；图2涂色部分的面积是58.88dm²．

点评：考查了圆环的面积和组合图形的面积，解题的关键是熟悉组合图形面积之间的和差关系．