
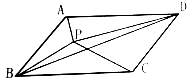
 如图.在平行四边形ABCD中.已知三角形ABP、BPC的面积分别是57、83.则三角形BPD的面积为16.
如图.在平行四边形ABCD中.已知三角形ABP、BPC的面积分别是57、83.则三角形BPD的面积为16. 分析 如图,过P作AB的平行线MN,则S△ABP和S△PCD分别是左右两个平行四边形面积的一半,S△BPC+S△PCD=S△BCD+S△BPD=12S平行四边形ABCD+S△BPD,S△ABP+S△PCD=12S平行四边形ABCD,两式相减得:(S△BPC+S△PCD)-(S△ABP+S△PCD)=S△BPD,S△BPD=S△BPC-S△ABP,从而求出三角形BPD的面积.
解答 解:如图,
过P作AB的平行线MN交BC于M,交AD于N,
则S△ABP的面积是S?ABMN一半,S△PCD是S?NMCD一半,
所以S△ABP+S△PCD=$\frac{1}{2}$S平行四边形ABCD…①,
由于S△BPC+S△PCD=S△BCD+S△BPD=$\frac{1}{2}$S平行四边形ABCD+S△BPD…②,
②减①得:(S△BPC+S△PCD)-(S△ABP+S△PCD)=S△BPD,
即S△BPD=S△BPC-S△ABP=83-57=26
故答案为:26.
点评 此题较难,关键是通过作辅助线,得知则S△ABP和S△PCD分别是左右两个平行四边形面积的一半,通过相等三角形面积的等量代换,最终求得三角形BPD的面积.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com