
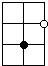
 这是一个棋盘,将一个白子和一个黑子放在棋盘线交叉点上,但不能在同一条棋盘线上.问:共有多少种不同的放法(如图)?
这是一个棋盘,将一个白子和一个黑子放在棋盘线交叉点上,但不能在同一条棋盘线上.问:共有多少种不同的放法(如图)?

 学业测评一课一测系列答案
学业测评一课一测系列答案科目:小学数学 来源: 题型:
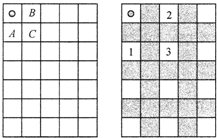 图是一个5×7的方格棋盘,左上角有1枚棋子.甲先乙后,两人轮流走这枚棋子,每人每次只能向下、向右或向右下走一格,如图中棋子可以走A、B、C三格之一.谁将棋子走入右下角方格中谁获胜.如果都按最佳方法走,那么谁将获胜?怎样走?
图是一个5×7的方格棋盘,左上角有1枚棋子.甲先乙后,两人轮流走这枚棋子,每人每次只能向下、向右或向右下走一格,如图中棋子可以走A、B、C三格之一.谁将棋子走入右下角方格中谁获胜.如果都按最佳方法走,那么谁将获胜?怎样走?查看答案和解析>>
科目:小学数学 来源: 题型:
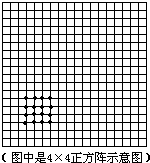 如图,这是一个围棋盘,还有一堆围棋子,将这堆棋子往棋盘上放,当按格点摆成某个正方阵时,尚多余12枚棋子,如果要将这个正方阵改摆成每边各加一枚棋子的正方阵,则差9枚棋子才能摆满.问:这堆棋子原有多少枚?
如图,这是一个围棋盘,还有一堆围棋子,将这堆棋子往棋盘上放,当按格点摆成某个正方阵时,尚多余12枚棋子,如果要将这个正方阵改摆成每边各加一枚棋子的正方阵,则差9枚棋子才能摆满.问:这堆棋子原有多少枚?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com