Question

10．如图，O是△ABC的重心，则图中面积相等的三角形有（　　）

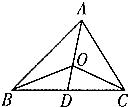
• A． 2对
• B． 3对
• C． 4对
• D． 5对

Answer 1

分析 延长BO、CO分别交AC、AB于点E、F，根据重心的定义：三角形三条中线的交点叫三角形的重心．可知D、E、F为三角形ABC各边中点，故得BD=CD，于是可得S_△ABD=S_△ACD=$\frac{1}{2}S$_△ABC，同理可知：S_△CBE=S_△ABE，S_△ACF=S_△BCF，都等于$\frac{1}{2}$S_△ABC，即可求出与△ABD面积相等的三角形的个数，解决问题．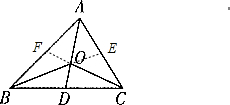

解答 解：因为O是△ABC的重心，
所以BD=CD，
又因为△ABD与△ADC等高，
所以S_△ABD=S_△ACD=$\frac{1}{2}S$_△ABC，
同理可知：S_△CBE=S_△ABE，S_△ACF=S_△BCF，（都等于$\frac{1}{2}$S_△ABC）
所以图中与△ABD面积相等的三角形个数为5个，
即S_△ABD=S_△ACD=S_△CBE=S_△ABE=S_△ACF=S_△BCF=$\frac{1}{2}$S_△ABC，
所以图中面积相等的三角形有3对．
故选：B．

点评 根据重心的定义：三角形三条中线的交点叫三角形的重心，可知BD=CD，然后根据三角形等底等高这一知识点，推出三角形面积之间的关系，从而解决问题．