
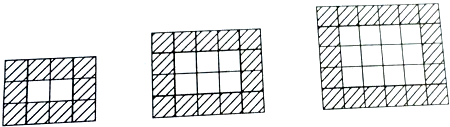
分析 ①第一个图形横行的块数是4,竖行的块数是3,第二个图形横行的块数是5,竖行的块数是4,第三个图形横行的块数是6,竖行的块数是5,以此类推,第n个图形横行的块数是(n+3),竖行的块数是(n+2);
②第一个图形中白色瓷块有1×2=2,黑色瓷块=2×5=10,第二个图形中白色瓷块有2×3=6,黑色瓷块=2×7=14,第三个图形中白色瓷块有3×4=12,黑色瓷块=2×9=18…那么依此类推第n个图形中有白色瓷块=n(n+1),黑色瓷块=2(2n+3),据此解答.
解答 解:①在第4个图中,横行应该有4+3=7块瓷砖.竖行有4+2=6块瓷砖;
②10×(10+1)=110(块)
2×(2×10+3)
=2×23
=46(块)
答:在第4个图中,横行应该有7块瓷砖.竖行有6块瓷砖.在第10个图中,一共有110块黑瓷砖,46块白瓷砖.
故答案为:7,6;110,46.
点评 解题的关键主要是寻找规律;再根据规律进行解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com