练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    11．图中，有（　　）组面积相等的三角形．
    A．一B．二C．三

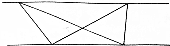
    分析 如下图所示，依据等底等高的三角形的面积相等，可知三角形ABC的面积等于三角形DBC的面积，三角形ADB的面积等于三角形ADC的面积，再利用等式的性质，这两组三角形中的任意一组减去它们重叠的部分，即可得到三角形ABO的面积等于三角形DCO的面积，据此即可得出结论．

    解答 解：

    如上图所示：
    因为等底等高的三角形的面积相等，
    所以三角形ABC的面积=三角形DBC的面积，三角形ADB的面积=三角形ADC的面积，
    再由等式的性质可得：三角形ABC的面积-三角形BOC的面积=等于三角形DBC的面积-三角形BOC的面积，
    即：三角形ABO的面积=三角形DCO的面积，
    综上，图中共有三组面积相等的三角形．
    故选：C．

    点评 本题主要考查了学生对三角形的面积公式的理解和灵活运用能力，要牢记等底等高的三角形面积相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：填空题

    1．圆柱和圆锥的体积相等，底面积也相等，圆柱的高是1.2米，圆锥的高是36分米．

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    2．零点五四六写作0.546，它是由5个0.1、4个0.01和6个0.001组成的．

    查看答案和解析>>

    科目：小学数学 来源： 题型：判断题

    19．850×60积的末尾共有2个0．×．（判断对错）

    查看答案和解析>>

    科目：小学数学 来源： 题型：判断题

    6．15×0.3和0.3×15的计算结果相同，表示的意义也相同．×（判断对错）

    查看答案和解析>>

    科目：小学数学 来源： 题型：判断题

    16．一升水和一升汽油一样重．×．（判断对错）

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    3．完成一件工作，甲用9天，乙用10天，甲的工效是乙的工效的$\frac{10}{9}$倍．

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    20．把一根6米长的铁丝平均分成7段，每段占全长的$\frac{1}{7}$，每段长$\frac{6}{7}$米．

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    1．期中测验后，五（2）班的3位同学向家长汇报成绩时说了下面的话：
    A同学说：“我们班的同学成绩有高有低，平均87分!”
    B同学说：“不在人前，不在人后．我得了90分，我是中等水平．”
    C同学说：“我得了93分，我们班得93分的人最多了!”
    请用所学知识说明该班的测验成绩．

    查看答案和解析>>

    同步练习册答案