
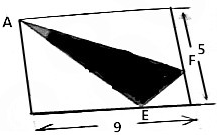
分析 因为图中△ABE、ADF和四边形AECF面积相等,因此可以用长方形ABCD的面积除以3得到△ABE、ADF和四边形AECF的面积;然后利用三角形的面积公式,已知三角形的面积和高,可以求出三角形的底,即BE和DF的长度,进而求出EC和CF的长度,然后利用三角形的面积公式求出三角形FEC的面积,再用四边形AECF的面积减去三角形FEC的面积即可.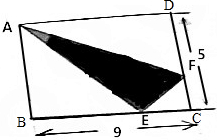
解答 解:△ABE、ADF和四边形AECF的面积是:9×5÷3=15(平方厘米)
BE=15×2÷5=6(厘米)
DF=15×2÷9=$\frac{10}{3}$(厘米)
所以CE=BC-BE=9-6=3(厘米)
CF=CD-DF=5-$\frac{10}{3}$=$\frac{5}{3}$(厘米)
所以三角形FEC的面积是:3×$\frac{5}{3}$÷2=2.5(平方厘米)
因此阴影部分的面积是:15-2.5=12.5(平方厘米).
答:阴影部分的面积是12.5平方厘米.
点评 解决本题的关键是求出△ABE、ADF和四边形AECF面积,并能灵活的利用三角形的面积公式求得某些线段的长度.


科目:小学数学 来源: 题型:解答题
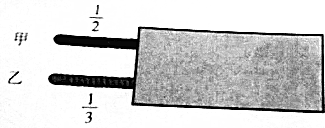 下面有甲、乙两条绳子,每条绳子都有一部分被纸挡住了,甲绳露出了它的$\frac{1}{2}$,乙绳露出了它的$\frac{1}{3}$,露出部分长度相等,哪条绳子长?你是怎样想的?
下面有甲、乙两条绳子,每条绳子都有一部分被纸挡住了,甲绳露出了它的$\frac{1}{2}$,乙绳露出了它的$\frac{1}{3}$,露出部分长度相等,哪条绳子长?你是怎样想的?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com