一根2米长的方木(侧面为正方形)锯成相等的三段后,表面积比原来增加36平方厘米,把其中的一段削成尽可能大的圆锥,这个圆锥的体积是多少立方厘米?
解:2米=200厘米,
方木的底面积为:36÷4=9(平方厘米),
根据正方形的面积公式:S=a×a,
9=3×3,
所以方木底面边长为3厘米,
根据底面的边长即是削成的最大圆锥的直径,
圆锥的底面积为:3.14×
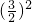
=7.065(平方厘米),
圆锥的高为:200÷3=

(厘米),
圆锥的体积为:

×7.065×

=2.355×

,
=157(立方厘米).
答:这个圆锥的体积是157立方厘米.
分析:根据题意可知,把长的方木锯成相等的三段后露出了4个底面,用36除以4可计算出一个底面的面积,再根据正方形的面积公式可得出底面正方形的边长,底面的边长即是削成的最大圆锥的直径,然后再根据圆的面积公式计算出这个圆锥的底面积,用2米除以3可得到这个圆锥的高,再利用圆锥的体积公式进行计算即可得到答案.
点评:解答此题的关键是确定最大圆锥的底面直径等于底面正方形的边长,然后再根据圆的面积公式、圆锥的体积公式进行计算即可.

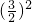 =7.065(平方厘米),
=7.065(平方厘米), (厘米),
(厘米), ×7.065×
×7.065×
 ,
,
